There has been good, there has been bad, but there is always busy.
Even a very simple post about mathematics, for example, takes a very long time to write. Time that I haven’t had available in a while.
But I do have time to help make the internet a safer, more secure place.
So I have set up a secure domain (rather painlessly thanks to my hosting company) and https://aelservices.ca is now a thing.
Certificate is from Let’s Encrypt!
So, I guess the take away is use a good hosting company (I like mine) and no excuse not to offer encryption, so, get on it.
A common early project for beginner programmers is a program to calculate and draw the Mandelbrot Set.
It’s a good project as the actual mathematics are simple, despite the fact that calculations are on the complex plane. Even if you’re not confident on basic algebra and geometry with complex numbers pretty well every programming language has libraries that will do all the real work for you anyway. Arguably, even if you don’t have an interest in the math involved itself, it’s still a good first project.
So, besides the actual calculation parts (I can say out of all the functions in my application, the actual calculation and value testing functions are the simplest by far) one has to work out how a user sets values they wish to change, how to write output to the screen and to files, including making and saving image files. It is a nice first complete application project.
It’s a project that covers the entire workflow, user input, data manipulation, output to user. Further, there are always improvements to try as you learn more. Most optimizing in one sense isn’t worth it (“Premature optimization is the root of all evil” – Donald Knuth. Take this advise to heart, you don’t know what needs optimizing until you have stable, working code to profile in the first place). However, a project like this isn’t for a client, so, feel free to break your code and resurrect it over and over. There are HUGE time savings to be found in there, and website after website discussing all sorts of tricks and tips. No reason for me to repeat what many have said far better than I could.
What I want to mention is data presentation. The Mandelbrot set image is actually communicating very little. If a pixel is black, the point it is representing is almost definitely in the set. If it is not black, the point it is representing is very likely not in the set. The only time membership is really in question is for points close to the boundary. How close do they have to be to the boundary to be questionable? Well, the more iterations you allow the program to try, the closer to the boundary you can go and consider the determination trustworthy. Even so, your computer is almost definitely using decimal approximations of the point in question (I guess if you had (eg) Maple do the symbolic manipulations the only time you touch an approximation is when you draw a pixel, but that is beyond the scope of this discussion), so there may be rounding errors leading your computer to present the wrong conclusion. Finally your pixel is a square region, but the point calculated is a singular location, so the farther from the centre of the pixel you go, the less reliable the colour of that pixel is. Clear as mud, I know.
So, hand-waving all that aside, you do have an image that is approximately correct. Since a pixel is just a number mapped to a colour, the colour mapped to is basically arbitrary.
Take RGB colour space for example. A colour is defined by three components, how much red, how much green and how much blue light to emit, each one taking a value from 0 to 255. You end up with a cube with area:
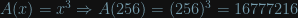
Since we can only have discrete values this give us our entire 24 bit colour space of 16,777,216 colours.
It would almost feel like you now have the only tool you need to do any colour manipulations you want. The space is well defined and closed under addition modulo 256 allowing cyclic behaviour. In fact one can further just choose a point within the space, use it to define one corner of a cube within the space centred around the colour space’s midpoint and you have all reflections and at least a few rotations available (or just allow reduction modulo 256 so any rotation that puts the point outside the colour space maps it back in. We have no need of a one to one mapping after all. The possibilities are endless (for finite values of endless) really). However, just ask an engineer about RGB space and they will tell you how happy they are that no display is actually built on that model. In the end, there is no natural way to navigate the space that is aesthetically pleasing, or even sensible.
Instead, and this is only one of several other colour spaces, let’s try a cylindrical coordinate system. A cylinder is made by taking a circular disk and drawing it through space perpendicular to its face. Let the hues all be represented as being at a given angle on the disk’s edge, so as you go around the curved surface you cycle through all available hues [Fun fact, you can do this since we perceive a colour we call magenta which does not actually exist as a discrete wavelength of light. The EM spectrum goes from red to violet, but if you present the human eye with a mix of red and voilet light we perceive magenta as if it were a distinct colour and further as one that fills the role of looping the colours around for us. Your brain is constantly lying to you and this fictional colour is one of my favourite examples]. Go up the cylinder, let it be as if you were turing up a light and the colours get lighter and eventualy wash out. Go down the cube, turn the light down until no illumination at the bottom and we have black. The the disk in the middle of the cylinder is optimum lighting. Finally, highest saturation is at the outside edge of the cylinder and saturation goes down as you approach the centre of the disk at the height you are at on the cylinder. So, all points in this space are defined by an angle (around the disk), a distance from the centre of the disk towards the edge, and a distance from the base to the desired height. This is a cartoon version of the HSL colour space (and I do mean cartoon since what I’m describing there is actually wrong since HSL is better understood as two cones rather than one cylinder, the wikipedia article is actually amazing and if you have the time and care, read through it).
Ok, now, we compare two images from the Mandelbrot set, both exact same region, same maximum iterations, same subsampling, same everything as I did one right after the other and all I did was change with colouring algorithms I used. The upper image is an RGB space colouring system that is sometimes ok, but, here really just does not give anything nice, and the bottom one is an HSL algorithm I wrote that ties magnitude to trigonometric functions with results that I think look neat.
Simple RGB cube, linear walk through space systematically.
HSL Mapping of colour space. Sinusoidal movement through space. Click on image for full size.
We have the exact same data, and the functions I built have the capacity to never cycle (as in if you want to make sure you don’t have a collision of two values to one colour, that is a setting I included) at which point the colours themselves do indeed have a one to one mapping for the data at the point in the centre of the pixel as my program calculated it. That is to say, both images are as information perfect as you can hope for here, it’s just one is far more compelling to the average viewer. Information preservation is just not enough to engage and inform.
The original intent was to have the output be the final animated gif file, but I never finished that aspect and just used GIMP to compile the stills.
The idea was just to have sine waves that emanated from given points and be able to accurately display the waves and in the case of multiple origins, the interference patterns.
Just think of them as being seen from above, white being crests and black being troughs. Now, this was around the same time as the Voronoi images so no surprise that different metrics where on my mind. I did the normal Euclidean distance but also threw in my favourite alternate metric, Manhattan distance.
So, some typical examples follow. These are the same sine waves, same amplitude, frequency and velocity, just different metrics.
Single origin, Euclidean distance sine wave. No drop off of amplitude here or in any of the animations shown below, although the software was capable of it. Basically you have expanding concentric circles here, nothing mind blowing.
Single origin, Manhattan distance sine wave. This is the same origin point, same frequency, amplitude and velocity, only the distance metric changes. Expanding concentric diamonds (or squares if you don't think standing a square on a point changes anything about it) replace the circles, but of the same thickness etc. A little neat, but nothing to write home about.
Dual origin, Euclidean distance sine waves, interfering. The two wave generators are producing waves of identical frequency, amplitude and velocity. A nice interference pattern looking exactly as one would expect.
Dual origin, Manhattan distance sine waves, interfering. So, this has the same origin points, same frequency, amplitude and velocity as the one just above, but Manhattan distance is used instead of the normal Euclidean distance. This is the exact same interference pattern as the one just above, but because of how the distance is calculated, we get this really neat patchwork effect. I discuss just a few of the key features after the cut.
A Voronoi diagram is a visual representation of relative distance between several points on the plane. For a given point on the plane (in most examples and in my examples below the point is coloured black) a colour is assigned, and all surrounding pixels to that point are coloured the assigned shade if they are closer to that point than to another. So, as you get further from a point eventually a given pixel is closer to another point than to the one we were first concerned with, and that pixel is coloured the assigned colour of that other point. So a given pixel is coloured black (usually, but no one can stop you from not doing so if you like) or is coloured the assigned colour of the nearest key point.
So, one can think of the solid colour areas as the area of influence of the point that colour was assigned to that is somewhere within that solid region. That is one way to think about it, see the wikipedia entry linked above for a far better explaination that I have supplied, along with a partial list of applications of these diagrams.
A while ago a friend of mine was talking about ways to tessellate 2 dimensional images for a certain effect he wanted. He was talking to me about this and mentioned he thought interpolating a given image as a Voronoi diagram could give him the effect he wanted if consistent reference points and colour mappings were possible. I wasn’t at the time familiar with these diagrams and read up on them. The first question was if an original image could be discerned from such a diagram, and I offered to throw together a quick proof of concept program (the friend in question is far and away a better programmer than I am, but I have been doing computer imagery for a long time and I also have a formal mathematics education whereas he does not. I still am deeply in his debt for his help in many of my projects).
Here is an example of what the first images we produced looked like.
This video describes exactly what mathematicians do and how applied number theory works.
In other words, it’s time for Numberwang!
(Clip from That Mitchell & Webb Look. I did not post the linked clip, so if anyone involved with the show wants the clip removed please contact Youtube directly. Also, one of the greatest comedy sketch shows ever made, so check it out if you get the chance.)
Let’s say I have a function that takes in a real number, adds the negative of one half that real number to itself and returns this new number. Now, take that new number and feed it in to the function. Repeat this as many times as you please and you can see that the output is tending towards zero. Here, zero is an attractor, and zero’s basin of attraction is the entire real number line, not including zero itself (for zero the value is fixed and that’s just boring). An attractor doesn’t have to be a single point, it can be a curve, or a set of a few discrete points, or whatever. A strange attractor is an attractor that is a fractal.
Well, that is at least the cartoon version, as we say.
So, on to that neat result. Let’s say that on the real plane you pick 3 distinct points. Here we will pick them such that they mark the corners of an equilateral triangle, but this is not necessary. Now, place a point at any finite value at all on the real plane. It doesn’t matter where, inside the three points, outside the three points, directly between two points, it doesn’t matter. Now, choose any one of those three points at random (we will call those special points corners). Draw a new point one half of the distance between that first random point and the chosen corner. Now, pick a corner at random, draw a new point half way between that last point and the new chosen corner. Repeat this as many times as you please. We are picking corners at random but a very regular shape starts to emerge.
The shape is this function’s strange attractor, which just happens to be Sierpinski’s Triangle. Sierpinski’s Triangle is classically made by taking an equilateral triangle, finding the midpoint of each side and removing the triangle described from those points from the triangle’s centre. Then do the same with all three new triangles you have. Then with all nine new triangles etc, an infinite number of times. Yet we can approach that same strictly defined shape using a process that is in fact dependent on randomness.
